Akaike's Information Criterion: AICの実装【python】【データ分析】

今日扱うのは赤池の情報量規準(Akaike's Information Criterion: AIC)です。最近データサイエンスなどでAICを耳にする方も多いと思います。図書館にもAICについての本が出ていました。これをPythonで実装するのを紹介したいです。

AICとは
AICとは
Pythonこのコードに使われているAICとLSMはこのサイトを参考にしました。
実行結果について
最後に

1．AICとは

2．Pythonコードと説明

3．実行結果について

4．最後に

AICとは

尤度とAIC

AICとは

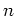次回帰モデルの最尤法の結果について改めて考えてみると，ある問題点に気が付く．それは次数が大きいほど残差平方和は小さくなることである．つまり，残差平方和が小さいことが正義だとすると，次数を大きくとることが正しいモデル選択の方法になってしまう．極論を言うと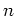組のデータを用いて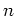次回帰モデルを作ることが一番よいモデルであるということになる．しかし，この考え方はどうみてもおかしい．赤池の情報量規準(Akaike's Information Criterion: AIC)は，このような問題点を回避するためのものさしとなるものである．

今回はこれを用いて実際のデータではないが、データ似合う最適の次数で表された関数をグラフ化し、関数を求めるコードを作りました。

Pythonこのコードに使われているAICとLSMはこのサイトを参考にしました。

import numpy as np
import scipy as sp
from scipy import integrate
import math
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import pyplot
from numpy.linalg import pinv

import AIC
import LSM

x=[1,2,2,3,3,4,5,6,7,12,13,15,15,18,20,21,24,27]
y=[3,3,5,12,6,4,8,13,16,19,22,19,11,7,3,9,14,19]
x1 = np.array(x)
y1=np.array(y)

plt.plot(x,y,'o')
num=5

data = np.array([x1,y1]).T

data_x=[]
data_y=[]
for i in data :
    data_x.append(i[0])
    data_y.append(i[1])

# データをプロット

for k in range(0,num):
    N = k
AIC_com=[]

for n in range(N+1):
    # 実行する次数
    print("N="+str(n))

    # LSMで誤差と重みベクトルcoeを計算
    error, coe = LSM.LSM(data, int(n+1))
    print("error:"+str(error))
    print("coe:"+str(coe[::-1]))

    # ここで，このモデルのAICを計算
    l = AIC.l_MAX(list(coe[::-1]),data_x,data_y)
    AIC_n = AIC.AIC(l,n+1)
    print("l="+str(l)+", AIC("+str(n)+")="+str(AIC_n))
    AIC_com.append(AIC_n)



Minimum = np.min(AIC_com)
for m in range(0,num):
    if AIC_com[m] == Minimum:
        print('AIC最小の次数は:{}次'.format(m))
        s = m
        print("N="+str(s))

    # LSMで誤差と重みベクトルcoeを計算
error, coe = LSM.LSM(data, int(s+1))
print("error:"+str(error))
print("coe:"+str(coe[::-1]))

    # ここで，このモデルのAICを計算
l = AIC.l_MAX(list(coe[::-1]),data_x,data_y)
AIC_s = AIC.AIC(l,s+1)
print("l="+str(l)+", AIC("+str(s)+")="+str(AIC_s))
AIC_com.append(AIC_s)
print(np.poly1d(coe))
    # LSMで得た近似線をプロット
test_3 = np.arange(min(data_x), max(data_x), 0.01)
plt.plot(test_3, LSM.quation_LSM(coe, test_3),color='black',label="Harp seal ($Pagophilus$ $groenlandicus$)" )

plt.title("AIC")
plt.xlabel('x value')
plt.xlim(0,30)
plt.ylim(0,30)
plt.show()